| Waar haalt Leon ter Beek het toch vandaan?! Hij komt met 3 schaakproblemen. 1. De eerste van een paus 2. De tweede van een beroemde schrijver 3. De derde, een moeilijke, is eigenlijk alleen geschikt voor Ton Snoeren, als hij tenminste een beetje oplet. |
29-1-2021: Deze keer heeft Leon voor elk wat wils aan schaakproblemen verzameld. Lees hieronder wat Leon er over weet te vertellen.
Amateurs en profs
door LtB
Deze keer laat ik meteen maar drie studies zien! Het gaat om twee studies van amateurs en één studie van een doorgewinterde puzzelaar.
De eerste studie werd in 1946 gepubliceerd door een Poolse schaakliefhebber die in datzelfde jaar tot priester werd gewijd. Zijn naam luidde: Karol Wojtyła. Tegenwoordig kennen wij deze schaakenthousiasteling beter onder zijn latere naam Paus Johannes Paulus II!
De opgave luidt: wit geeft mat in 2.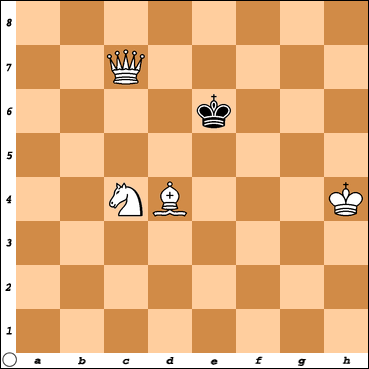
Diagram 1 (Woytiła 1946): wit geeft mat in 2.
Vervolgens zien we een studie die in 1970 is gepubliceerd door Vladimir Nabokov, de geniale Russische schrijver van onder andere boeken als Lolita, Pnin en The Defense. Dat laatste boek beschrijft het tragische leven van de fictieve schaker Loezjin. Ook Nabokov was een fervent liefhebber van het schaakspel. De studie verscheen in Poems and Problems uit 1970. De opgave luidt: wit geeft mat in 3.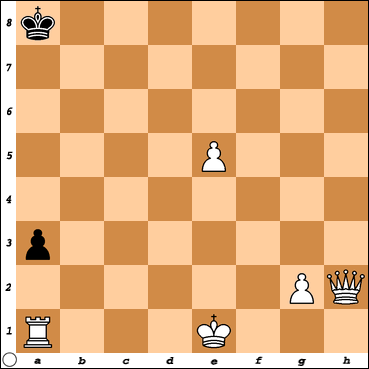
Diagram 2 (Nabokov 1970): wit geeft mat in 3.
Tenslotte, ter afsluiting, het zwaardere werk. Het betreft een studie van de befaamde Amerikaanse probleemcomponist Sam Loyd, gepubliceerd in 1859 in Chess Monthly. Dit juweeltje van een studie staat op een veel hoger niveau dan de eerste twee, dus wees gewaarschuwd! De opgave luidt: wit geeft mat in 5 zetten.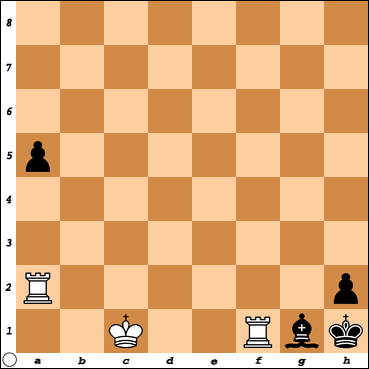
Diagram 3 (Loyd 1859): wit geeft mat in 5.
Ik ontleen de studies aan het boek van Colin Russ, Schaakminiaturen uit vele landen. 400 miniatuurschaakproblemen met oplossingen en commentaren, Amsterdam 1983.
De eerste twee studies zijn wel te doen; op de derde kan men zijn tanden stukbijten. Veel plezier ermee!
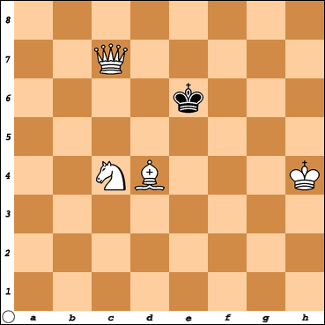
De oplossing van het pausprobleem:
1.Pd2 Kd5
2 Dd7 mat.
Dat was een makkelijke….
Juist! Er is overigens nog een tweede variant: als zwart niet 1… Kd5 maar 1… Kf5 speelt, zet wit mat middels 2. Df5#.
Herstel: ik bedoel uiteraard 2. Df7#!
Ik geef weer een tip voor de oplossing van het probleem van Nabokov: de eerste zet is een damezet.
De penningmeester van HMC heeft mij een mailtje gestuurd met de correcte en volledige oplossing van de problemen van Nabokov en zelfs die van Loyd! Respect… Kan iemand van onze club de oplossing ook vinden?
Ik wacht ff tot anderen ook een poging wagen…
Hierbij geef ik de oplossingen!
Eerst het probleem van Nabokov. De eerste zet is 1. Dh7! Hierna heeft zwart twee mogelijkheden: na 1… Kb8 volgt 2. Txa3 Kc8 3. Ta8# en op 1… a2 volgt 2. Db1! Ka7 3. Txa2#.
Het probleem van Loyd is veel moeilijker. Er spelen verschillende thema’s een rol.
De eerste zet is 1. Taf2. Hiermee zorgt wit ervoor dat de lijn van de toren die g2 dekt, niet wordt afgesloten als de koning later op d2 komt. Met andere woorden: wit voorkomt ‘interferentie’ (’tussenbeide komen’), zoals het afsluiten van een lijn door een stuk van eigen kleur wordt genoemd.
Zo’n zet die het afsluiten van een lijn voorkomt door een stuk over en voorbij een veld te brengen waarop dit zou gebeuren, heet een ‘antikritische zet’; het veld in kwestie (hier d2) wordt het ‘kritische veld’ genoemd.
Zwarts gedwongen eerste zet is 1… a4. Wit speelt daarop 2. Kd2, waarna zwart weer maar één zet heeft, en wel 2… a3.
Na deze zet beoogt wit interferentie van zijn andere toren (op f1) tot stand te brengen om de zwarte loper te ontpennen en zo de bescherming van de zwarte koning weg te nemen.
Met dat doel wordt de andere toren met een ‘kritische zet’ voorbij het kritische veld (e1) gebracht, en wel middels 3. Ta1.
Na de gedwongen zet 3… a2 bereikt wit de gewenste interferentie door middel van 4. Ke1. Na het gedwongen antwoord van zwart, 4… Lxf2+, staan twee stukken van wit zodanig op één lijn met de vijandelijke koning, dat het verstverwijderde (de toren) hem schaak zal geven als het dichtstbijzijnde (de koning) opzij gaat; dit heet een ‘directe batterij’ (een ‘indirecte batterij’ is gericht op een veld vlak naast de zwarte koning). Voor de vierde zet van zwart is de batterij nog ‘gemaskeerd’, zoals dat heet (door zijn loper op g1). In dit probleem is sprake van een ‘koningsbatterij’ omdat wit zijn koning gebruikt. Wit zet de kroon op het werk met 5. Kxf2#.
De volledige oplossing luidt dus:
1. Taf2 a4 2. Kd2 a3 3. Ta1 a2 4. Ke1 Lxf2+ 5. Kxf2.
Deze oplossing is, zoals gezegd, gevonden door P. van Helvoort, de penningmeester van HMC. Knap gedaan!